Bit Manipulation : A Simple Example

Background
What are Bitmasks?
Bitwise Operators
Shift Left and Shift Right (<< and >>)
A Sample Problem
1. Problem Statement
2. Insights
Conclusion

Background

I (in)frequently check on sites like Codeforces and Kattis to improve my programming logic and skills. One day, I stumbled upon an interesting problem to me. At first, this problem looked quite challenging, so I tried to solve it (problem will be explained in later sections). At first, I couldn’t solve it — I couldn’t find any patterns relating to the problem. I wasn’t in such a rush, so I left the problem as it’s already midnight.

Once I was doing nothing at the shopping mall. I went to look back at the problem, and I got an idea on how to do it - which is by using bit manipulation!

What are Bitmasks?

In order to understand bit manipulation, firstly we need to understand bitmasks since it is used in bit manipulation operations. A bit is short of "binary digits" - digits which contains zeros and ones. An integer variable usually have a 32 bits limit, which means it consists of 32 bits with its range of $2^{32}$ (2 derived from the state of bits — 0 or 1 which is 2 possibilities).

Bitmasks, on the other hand, are simply integers used as a set of booleans. Since booleans have a state of only False or True, it can also be represented by $0$ and $1$ , and that is why it is called bitmasks! Summing up:

Bitmasks take advantage of how an integer be represented in its binary form, meaning that it can be used as a compact set of booleans.

Bitwise Operators

Bit manipulation is a technique that is used to, well, manipulate the bits that represents an integer. I’m going to show you some commonly used bitwise operators in C++. This only shows the bit operators and how it works; the usage will be shown in the example. It’s uncommon to use it purely like in the examples (unless you work in low-level programming maybe).

Shift Left and Shift Right (`<<` and `>>`)

This operation shifts the binary form of an integer to left/right given the value.

Note that shift left is equivalent to multiplying by 2, and shift right is dividing by 2 and rounding it. It’s generally faster than usual dividing operations altough the compiler may already compiled it to use shift operations.

int x=5; // 101 in binary

x=5;
x=x<<1; //10 = 2 in decimal

x=5;
x=x<<3; //0 = 0 (can be seen as 0101)

x=5;
x=x>>1; //1010 = 10 in decimal

x=5;
x=x>>2; //10100 = 20 in decimal

Bitwise OR (`|`)

Does OR operation on the binary form of two integers bit by bit.

int x=5; // 101 in binary
int y=9; // 1001 in binary
int z=x|y;

/*
x = 0101
y = 1001
--------- OR
z = 1101 = 13 in decimal
*/

Bitwise AND (`&`)

Does an AND operation on the binary form of two integers bit by bit.

int x=5; // 101 in binary
int y=9; // 1001 in binary
int z=x&y;

/*
x = 0101
y = 1001
--------- AND
z = 0001 = 1 in decimal
*/

Bitwise NOT (`~`)

This operator inverts the bits of the binary form of an integer. This operation is usually used in conjunction of other operators; for example to make an NAND or NOR operations.

No examples provided here since it depends on the data type.

Bitwise XOR (`^`)

Applies the XOR operation of the binary form of two integers bit by bit. Useful to toggle bits; see example below.

int x=5; // 101 in binary
int y=9; // 1001 in binary
int z=x^y;

/*
x = 0101
y = 1001
--------- XOR
z = 1100 = 12 in decimal
*/

You may seen a neat trick to swap two integers using XOR. It uses XOR's property to achieve so.

int a=3;
int b=5;

a=a^b; // a=6, b=5
b=a^b; // a=6, b=3
a=a^b; // a=5, b=3

A Sample Problem

Refer to this Kattis problem.

Problem Statement

Abridged problem statement: Given an infinite binary tree; each node consists of a fraction with numerator $p$ and a denominator $q$ . The left child node is equal to $\frac{p}{p + q}$ , and the right child node is equal to $\frac{p + q}{q}$ . A function $F (n)$ is defined such that it will return the fraction from the respecting node. The nodes is numbered as depicted in the illustration taken from the problem below:

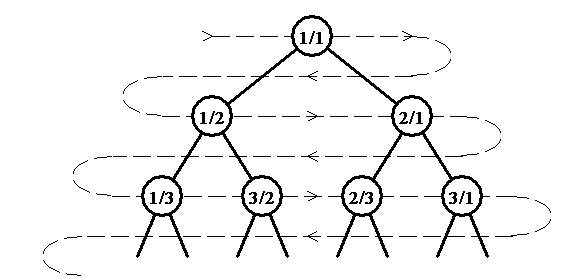
In the illustration above, the root node starts from the value of $p = 1$ and $q = 1$ . This means that $F (1) = \frac{1}{1}$ , $F (2) = \frac{1}{2}$ , $F (3) = \frac{2}{1}$ , etc. Given $p$ and $q$ , we are required to return the value of $N$ of which $F (n)$ corresponds to $\frac{p}{q}$ .

At a glance, this problem may not represent anything related to bit manipulation. If you look closer, it actually has two states - going to the left or right node (because of binary tree)! Before I give you my perspective on this problem, you may want to try and solve it for yourself 😀

Insights

The problem may suggest you to use breadth first search (BFS) method, by using a queue. For a fraction that lies in a small N, this would be viable. However, we don’t know where the inputted fraction would lie, as this is an infinite binary tree.

So, how can we solve the problem? Here’s my thought process:

It is (somehow) better to find directly from each testcase compared to pruning, as it would take too much time and memory.
We can represent each node with its binary form.
$p < q$ in the left nodes, whilst $p > q$ in the right nodes.

Q: What does it mean by using its binary form?

Well, let’s take the first, second, and third node in their binary form (1, 10, 11). Analyzing the pattern, we can first assume that in the left nodes we append a 0 from the first node, and in the right nodes we append a 1 from the first node.

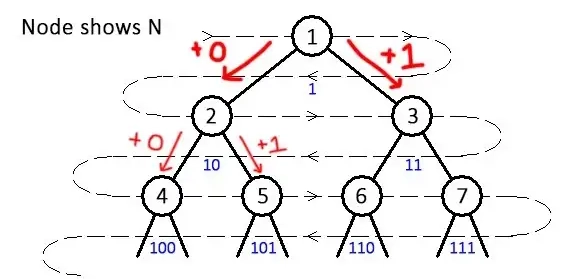
Q: Why does it work?

Simple — It is a binary tree! Well of course the N would follow the pattern of binary digits!

Because we’re solving the problem from by top-down, we need to append digits (if left 0, if right 1) from the front. How do we achieve such result? We use the OR operator with the shift left operator to turn on a bit in specified location.

int result=0; // 000
int pos=2;
result|=(1<<pos); //turning on the 2nd bit from the right (0-based)

/*
(1<<pos) = 1 << 2 = 100 (in binary)
result = 000

000
100
---- OR
100
*/

This is my solution written in C++:

#include<bits/stdc++.h>

using namespace std;

int main() {

  int t;
  scanf("%d", &t);

  while (t--) {
    int k;
    int p, q;
    scanf("%d %d/%d", &k, &p, &q);

    int res = 0, cnt = 0;
    while (!(p == 1 && q == 1)) {
      int tp, tq;
      if (p > q) //right
      {
        tp = p - q;
        tq = q;
        res |= (1 << cnt);
      } else //left
      {
        tp = p;
        tq = q - p;
      }
      cnt++;
      p = tp;
      q = tq;
    }

    res |= (1 << cnt);
    printf("%d %d\n", k, res);
  }
}

Note that because we start from the index of one, we append another 1 after we reach the initial node.

This solution, because we traverse up a binary tree, it makes the time complexity of the program of $O (lo g n)$ .

Conclusion

This problem sample is just one of the usage of bit manipulation. Some other applications are also interesting in programming includes:

Storing boolean values in bitset
Reverse Backtracking by using Bitmasks
Dynamic Programming with Bitmasks
etc.

I hope this guide can be a good start to understand bit manipulation techniques, or enrich the readers with more knowledge.

Thank you for reading and happy learning 😀